Eksponen Dan Logaritma(3)
Materi Berkaitan dengan Logaritma
Untuk Kelas X MA/SMA
Logaritma adalah invers dari perpangkatan. Misalkan kita kita diberikan persamaan , bagaimana kita mencari harga
, bagaimana kita mencari harga  ? kebanyakan kita langsung dapat menjawab 3, tetapi bagaimana jika bentuk persamaannya adalah
? kebanyakan kita langsung dapat menjawab 3, tetapi bagaimana jika bentuk persamaannya adalah  dapatkah kita dengan mudah menentukan berapa nilai
dapatkah kita dengan mudah menentukan berapa nilai  ?
?
Untuk mengatasi permasalahan di atas kita membutuhkan kebalikan(invers) dari perpangkatan tersebut, yaitu Logaritma yang selanjutnya disebut dengan “Log”
Perhatikan bahwa
Untuk dan
dan  ,
,
maka berlaku:
dengan:
 = bilangan pokok/basis
= bilangan pokok/basis
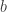 = numerus (bilangan yang dicari nilai logaritmanya,
= numerus (bilangan yang dicari nilai logaritmanya,  )
)
 = hasil logaritma
= hasil logaritma
Sifat-sifat operasi aljabar pada logaritma
Contoh 1
Nyatakan dalam logaritma
Jika diketahui , maka tentukan
, maka tentukan
Sederhanakanlah untuk
Jawab:

Contoh 4
(UN Mat IPA 2012) Jika diketahui dan
dan  , maka nilai
, maka nilai  = ….
= ….
Jawab:

Contoh 5
Jika , maka nilai
, maka nilai  yang memenuhi adalah ….
yang memenuhi adalah ….
Jawab:
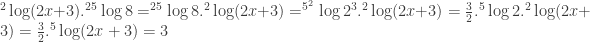
Sehingga

Soal Latihan
Untuk Kelas X MA/SMA
Logaritma adalah invers dari perpangkatan. Misalkan kita kita diberikan persamaan
Untuk mengatasi permasalahan di atas kita membutuhkan kebalikan(invers) dari perpangkatan tersebut, yaitu Logaritma yang selanjutnya disebut dengan “Log”
Perhatikan bahwa
Untuk
maka berlaku:
dengan:
Sifat-sifat operasi aljabar pada logaritma
Contoh 1
Nyatakan dalam logaritma
Jika diketahui
Sederhanakanlah untuk
Jawab:
Contoh 4
(UN Mat IPA 2012) Jika diketahui
Jawab:
Contoh 5
Jika
Jawab:
Sehingga
Soal Latihan
- Tentukanlah nilai dari a)
, b)
, c)
, d)
, dan e)
- (UN Mat IPA 2014) Nilai dari
- Sederhanakanlah
- (UN Mat IPA 2014) Nilai dari
- (UN Mat IPA 2014) Hasil dari
- Carilah nilai
dari persamaan
- Sederhanakanlah
- Jika
dan
, maka nilai dari
- Jika
dengan
, maka nilai dari
- (UM IKIP PGRI 2010) Tentukanlah nilai
dari persamaan
- Jika diketahui
, maka nilai
- (OSN Mat SMA Tk Kab 2014) Misalkan
dan
. Jika
,
, dan
, maka nilai dari
Tidak ada komentar:
Posting Komentar