Sistem Persamaan dan Pertidaksamaan Linier
A. Sistem Persamaan Linier
Sistem Persamaan Linier Dua Variabel adalah sistem persamaan linier yang mempunyai bentuk

dengan adalah bilangan real
adalah bilangan real
B. Hubungan Dua Buah Garis Lurus(Sistem Persamaan Linier Dua Variabel)
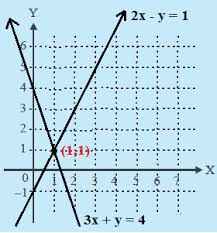 dan
dan 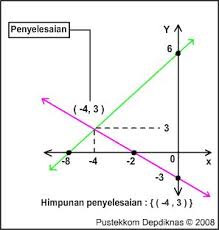
[Sumber]

1.Penyelesaian sistem persamaan adalah ….
adalah ….
Jawab:
perhatikan untuk
Untuk persamaan 2) x= 6 + 2y kita substitusikan ke persamaan 1). Selanjutnya kita mendapatkan
Kemudian persamaan 3) disubstitusikan ke persamaan 2), maka akan didapatkan x = 2.
Jadi penyelesaian sistem persamaan tersebut adalah
2. Jika diketahui x dan y memenuhi sistem persamaan dan
dan  , maka nilai
, maka nilai  = ….
= ….
Jawab:
Dengan cara kurang lebih sama dengan pembahasan soal pada contoh no 1) di atas tetapi dengan gabungan eliminasi dan substitusi. Misalkan

—————————————————— +

Jadi, nilai
3. Enam tahun yang lalu, umur Budi 4 tahun lebih muda dari seperenam umur ayahnya. Jika umur Budi sekarang 3 tahun lebih tua dari seperdelapan umur ayahnya, maka jumlah umur mereka berdua sekarang adalah ….
Jawab:
Misalkan umur Budi = x , dan umur ayahnya = y , maka persoalan di atas dapat dimodelkan sebagai berikut

Jadi, jumlah umur mereka adalah 48 + 9 = 57 tahun.
C. Sistem Persamaan Linier Tiga Variabel
Sistem persamaan ini memiliki bentuk

Untuk ketentuan yang lain kurang lebih sama seperti sistem persamaan linier dua variabel

1. Himpunan penyelesaian sistem persaman

adalah {(x,y,z)}. Nilai untuk x + y + z = ….
Jawab:
Perhatikan bahwa

Persamaan 2) disubsitusi ke persamaan 3)
 . Kemudian persamaan 2) dan 4) dijumlahkan. Selanjutnya kita mendapatkan
. Kemudian persamaan 2) dan 4) dijumlahkan. Selanjutnya kita mendapatkan  .
.
2. (OMITS SMP/MTs 2012) Ada 3 bilangan bulat. Jika masing-masing bilangan itu dipasangkan maka akan didapatkan jumlah 2006, 2010, dan 2012. Jumlah bilangan terbesar yang dimaksud adalah ….
Jawab:
Misalkan bilangan yang dimaksud adalah a, b, dan c, maka

Selanjutnya jumlahkan ketiga persamaan tersebut di atas. Sehingga kita mendapatkan

Maka bilangan terbesarnya adalah saat
(yakni persamaan ke 4) dikurangi persamaan pertama)

Perhatikan ilustrasi soal berikut
Misalkan suatu ketika seseorang sebut saja pak Ahmad berencana membangun 2 tipe rumah, yaitu, tipe A dan tipe B di atas sebidang tanah seluas 10.000 . Setelah ditanyakan kepada seorang arsitek ternyata untuk membangun rumah tipe A dibutuhkan tanah seluas 100
. Setelah ditanyakan kepada seorang arsitek ternyata untuk membangun rumah tipe A dibutuhkan tanah seluas 100  dan untuk rumah tipe B dibutuhkan tanah seluas 75
dan untuk rumah tipe B dibutuhkan tanah seluas 75  . Karena keterbatasan dana, akhirnya yang akan dibangun paling banyak 125 unit rumah saja, maka
. Karena keterbatasan dana, akhirnya yang akan dibangun paling banyak 125 unit rumah saja, maka
1) berapa banyak rumah tipe A dan tipe B yang harus dibangun sesuai dengan kondisi luas tanah yang tersedia dan jumlah rumah yang akan dibangun oleh pak Ahmad
2) gambarkanlah daerah penyelesaian pada koordinat kartesius berdasarkan batasan-batasan yang telah diberikan
Jawab:
Dimisalkan: x : banyak rumah tipe A yang segera dibangun
y : banyak rumah tipe B yang segera dibangun
1) Banyaknya rumah tipe A dan tipe B yang akan dibangun

Dengan mengalikan x + y = 125 dengan 3 kemudian dieliminasikan ke 4x + 3y = 400 diperoleh

untuk , maka
, maka 
Hal ini menunjukkan bahwa pak Ahmad dapat membangun rumah tipe A sebanyak 25 unit dan rumah tipe B sebanyak 100 unit.
2) Untuk gambar grafiknya pada bidang kartesius, kita perlu menentukan beberapa titik potong
untuk persamaan garis maka
maka 

untuk persaman maka
maka 

Selanjutnya buatlah titik uji, misalkan saja titik (0,0), kemudian kita substitusikan ke pertidaksamaan maupun
maupun  . Kalau hasilnya memenuhi maka daerah titik (0,0) termasuk penyelesaian.
. Kalau hasilnya memenuhi maka daerah titik (0,0) termasuk penyelesaian.
Silahkan kamu memasukkan titik uji yang lain
Dan akhirnya kita akan mendapatkan gambar grafik diagram kartesius sebagai berikut:

Sistem Persamaan Linier Dua Variabel adalah sistem persamaan linier yang mempunyai bentuk
dengan
B. Hubungan Dua Buah Garis Lurus(Sistem Persamaan Linier Dua Variabel)
- Jika kedua garis berpotongan, maka sistem persamaan linier memiliki sebuah penyelesaian. Hal ini terjadi jika
- Jika kedua garis sejajar, maka sistem persamaan linier tidak memiliki penyelesaian. Hal ini jika
- Jika kedua garis itu berimpit, maka memiliki tak terhingga penyelesaian. ini terjadi saat
 dan
dan 
[Sumber]
1.Penyelesaian sistem persamaan
Jawab:
perhatikan untuk
Untuk persamaan 2) x= 6 + 2y kita substitusikan ke persamaan 1). Selanjutnya kita mendapatkan
Kemudian persamaan 3) disubstitusikan ke persamaan 2), maka akan didapatkan x = 2.
Jadi penyelesaian sistem persamaan tersebut adalah
2. Jika diketahui x dan y memenuhi sistem persamaan
Jawab:
Dengan cara kurang lebih sama dengan pembahasan soal pada contoh no 1) di atas tetapi dengan gabungan eliminasi dan substitusi. Misalkan
—————————————————— +
Jadi, nilai
3. Enam tahun yang lalu, umur Budi 4 tahun lebih muda dari seperenam umur ayahnya. Jika umur Budi sekarang 3 tahun lebih tua dari seperdelapan umur ayahnya, maka jumlah umur mereka berdua sekarang adalah ….
Jawab:
Misalkan umur Budi = x , dan umur ayahnya = y , maka persoalan di atas dapat dimodelkan sebagai berikut
Jadi, jumlah umur mereka adalah 48 + 9 = 57 tahun.
C. Sistem Persamaan Linier Tiga Variabel
Sistem persamaan ini memiliki bentuk
Untuk ketentuan yang lain kurang lebih sama seperti sistem persamaan linier dua variabel
1. Himpunan penyelesaian sistem persaman
adalah {(x,y,z)}. Nilai untuk x + y + z = ….
Jawab:
Perhatikan bahwa
Persamaan 2) disubsitusi ke persamaan 3)
2. (OMITS SMP/MTs 2012) Ada 3 bilangan bulat. Jika masing-masing bilangan itu dipasangkan maka akan didapatkan jumlah 2006, 2010, dan 2012. Jumlah bilangan terbesar yang dimaksud adalah ….
Jawab:
Misalkan bilangan yang dimaksud adalah a, b, dan c, maka
Selanjutnya jumlahkan ketiga persamaan tersebut di atas. Sehingga kita mendapatkan
Maka bilangan terbesarnya adalah saat
(yakni persamaan ke 4) dikurangi persamaan pertama)
- Diketahui sistem persamaan
. Nilai
adalah ….
- Penyelesaian sistem persamaan
adalah ….
- Di sebuah toko, Aziz membeli 3 buku dan 2 buah pensil seharga Rp5.200,00. Sedangkan Fatimah membeli 2 buku dan 3 pensil seharga Rp4.800,00. Harga 1 buku adalah ….
- Jika jumlah dua bilangan adalah 67 dan selisihnya adalah 45, maka kedua bilangan tersebut adalah ….
- Sebuah bilangan terdiri dari dua angka yang besarnya 7 kali jumlah angka-angkanya. Jika kedua angka dipertukarkan, akan diperoleh bilangan baru, 18 lebih dari jumlah angka-angkanya. Bilangan yang dimaksud adalah ….
- Jika pembilang dan penyebut sebuah pecahan, keduanya dikurangi 5, akan diperoleh pecahan sama dengan
. Bila pembilang dan penyebut keduanya ditambah dengan 1, pecahan itu sama dengan
. Pecahan yang dimaksud adalah ….
- Para bola
melalui titik (1,1), (-1,-5), dan (3,23). Tentukanlah nilai a, b, dan c
- Jika diketahui sistem persamaan linier:
- Enung, Untung. 2009. Mandiri Matematika SMAjilid 1 Untuk Kelas X. Jakarta: Erlangga.
- Sukino. 2004. Persiapan Menghadapi Olimpiade Matematika Tingkat SMP Seri B. Jakarta: BSD MIPA.
Perhatikan ilustrasi soal berikut
Misalkan suatu ketika seseorang sebut saja pak Ahmad berencana membangun 2 tipe rumah, yaitu, tipe A dan tipe B di atas sebidang tanah seluas 10.000
1) berapa banyak rumah tipe A dan tipe B yang harus dibangun sesuai dengan kondisi luas tanah yang tersedia dan jumlah rumah yang akan dibangun oleh pak Ahmad
2) gambarkanlah daerah penyelesaian pada koordinat kartesius berdasarkan batasan-batasan yang telah diberikan
Jawab:
Dimisalkan: x : banyak rumah tipe A yang segera dibangun
y : banyak rumah tipe B yang segera dibangun
1) Banyaknya rumah tipe A dan tipe B yang akan dibangun
- Dari soal diketahui luas bidang tanahnya adalah 10.000
, maka model matematikanya adalah
. Selanjutnya kita sederhanakan menjadi
…………………………….(1)
- Dan jumlah rumah yang segera dibangun, dimodelkan sebagai
…………………………………..(2)
- Sebagai tambahannya, baik x dan y minimal adalah nol (kondisi dimana apabila kedua tipe rumah tersebut tidak jadi dibangun)
Dengan mengalikan x + y = 125 dengan 3 kemudian dieliminasikan ke 4x + 3y = 400 diperoleh
untuk
Hal ini menunjukkan bahwa pak Ahmad dapat membangun rumah tipe A sebanyak 25 unit dan rumah tipe B sebanyak 100 unit.
2) Untuk gambar grafiknya pada bidang kartesius, kita perlu menentukan beberapa titik potong
untuk persamaan garis
untuk persaman
Selanjutnya buatlah titik uji, misalkan saja titik (0,0), kemudian kita substitusikan ke pertidaksamaan
Silahkan kamu memasukkan titik uji yang lain
Dan akhirnya kita akan mendapatkan gambar grafik diagram kartesius sebagai berikut:

Tidak ada komentar:
Posting Komentar