LIMIT FUNGSI ALJABAR UNTUK X ~>a
Dasar untuk mempelajari kalkulus adalah konsep limit fungsi, yaitu limit fungsi aljabar dan limit fungsi trigonometri. Dalam topik ini kalian akan mempelajari materi Limit Fungsi Aljabar untuk x -> a.
Apakah kalian masih ingat bentuk bentuk fungsi polinomial (suku banyak), fungsi rasional (bentuk pecahan) dan fungsi irasional (bentuk akar)?
Bentuk bentuk fungsi itulah yang nanti akan kita limitkan dalam materi Limit Fungsi Aljabar ini.
Pengertian
Limit (nilai batas) adalah pendekatan terhadap suatu nilai atau harga tertentu. Jadi, harga batas (limit) bukanlah harga yang sebenarnya melainkan harga yang mendekati saja.
Bentuk umum penulisan
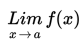
artinya menghitung nilai fungsi f(x) untuk nilai x mendekati nilai a.
Contoh 1
Diketahui f(x) = x + 3, dengan x ∈ R
Hitung nilai limit fungsi f(x) untuk x mendekati 2.
Hitung nilai limit fungsi f(x) untuk x mendekati 2.
Penyelesaian :
Penulisan limit secara matematis untuk soal di atas adalah :
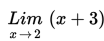
Nilai-nilai fungsi f(x) = x + 3 di sekitar x = 2 disajikan dalam tabel berikut :
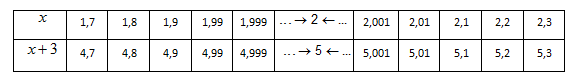
Dari tabel di atas kita lihat bahwa nilai f(x) = x + 3 mendekati nilai 5 ketika nilai x mendekati 2, baik dari arah sisi kiri maupun dari arah sisi kanan.
Dengan demikian,
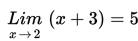
Contoh 2
Diketahui
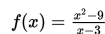
dengan x ∈ R dan x ≠ 3
Hitung nilai limit fungsi f(x) untuk x mendekati 3.
Penyelesaian :
Nilai-nilai fungsi
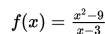
di sekitar x = 3 disajikan dalam tabel berikut :
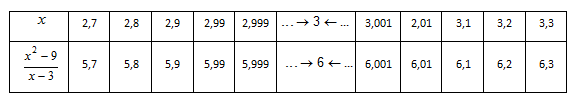
Dari tabel di atas kita lihat bahwa nilai
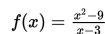
mendekati nilai 6 ketika nilai x mendekati 3.
Dengan demikian,
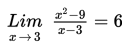
Contoh 3
Diketahui
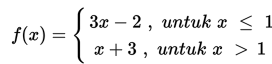
Hitung nilai limit fungsi f(x) untuk x mendekati 1.
Penyelesaian :
Nilai-nilai fungsi f(x) di sekitar x = 1 disajikan dalam tabel berikut :
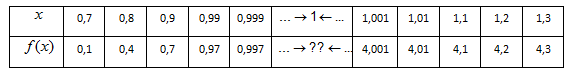
Dari tabel di atas kita lihat bahwa untuk nilai x -> 1, nilai fungsi f(x) tidak menuju ke satu nilai tertentu (ketika didekati dari arah sisi kiri, f(x) mendekati nilai 1 dan ketika didekati dari arah sisi kanan, f(x) mendekati nilai 4).
Dengan demikian,
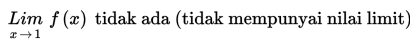
Langkah-langkah menghitung nilai limit untuk x -> a
(1) Masukkan/substitusikan nilai x = a, jika ada nilainya maka nilai itu adalah nilai limitnya.
(2) Jika setelah dimasukan nilai x = a diperoleh nilai nol per nol atau nol pangkat nol , maka ditempuh :
• jika f(x) dapat difaktorkan, maka faktorkan
• jika f(x) dalam bentuk akar, maka rasionalkan dengan cara mengalikan dengan bentuk sekawannya
• jika f(x) dalam bentuk akar, maka rasionalkan dengan cara mengalikan dengan bentuk sekawannya
Contoh 4
Hitung nilai
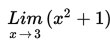
Penyelesaian :
Dengan mensubstitusikan nilai x = 3 diperoleh :
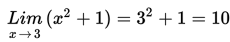
Contoh 5
Hitung nilai
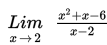
Penyelesaian :
Dengan mensubstitusikan x = 2 diperoleh :
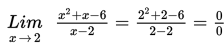
Karena diperoleh nol per nol, maka langkah selanjutnya dengan cara memfaktorkan pembilangnya :
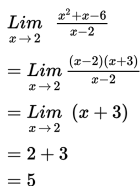
Contoh 6
Hitung nilai
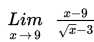
Penyelesaian :
Dengan mensubstitusikan x = 9 diperoleh :
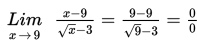
Karena diperoleh nol per nol, maka langkah selanjutnya dengan cara mengalikan dengan sekawan dari bentuk akarnya.
Dengan demikian,
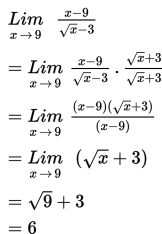
Tidak ada komentar:
Posting Komentar