Trigonometri
A. Tentang Sudut
Sudut adalah pertemuan atau perpotongan 2 buah garis/sinar atau bangun yang dibentuk oleh dua garis yang yang berpotongan di sekitar titik potongnya.
Untuk ukuran sudut, kita mengenal ada beberapa macam, yaitu: derajat, radian, gone/grade.
.
Perhatikan ilustrasi berikut
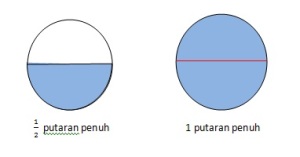
Selanjutnya yang sering dikenalkan adalah sudut dalam ukuran derajat dan radian.
Sebagai catatan:
Ukuran derajat yang diubah ke menit atau detik yang selanjutnya disebut dengan sistem seksagesimal, yaitu:
1 derajat = 60 menit = 3600 detik, atau
.
.
1. .
2.
3. Jadikanlah sudut dalam seksagesimal!
4. Jadikanlah sudut dalam satuan derajat!
Jawab:
1. Perhatikanlah
.
Kaadang dituliskan untuk , tinggal kita masukkan saja sebagai ganti pi di atas.
2. Dengan cara mirip dengan no.1, yaitu
.
3. Kita ingin menjadikan sudut dari ukuran derajat yang mengandung desimal ke seksagesimal.
Perhatikan langkahnya
.
4. Dengan cara yang kurang lebih sama, yaitu
.
.
.
B. Perbandingan Sudut dalam Segitiga Siku-Siku
Perhatikanlah ilustrasi berikut ini
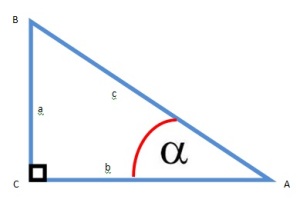
.
Untuk Perbandingan Sudut istimewa amati tabel berikut, khususnya sudut .
.
Karena pada segitiga siku-siku berlaku teorema Pythagoras, maka ada baiknya kita ingat-ingat tripel Pythagoras di sini yang sering digunakan/dimunculkan .
.
1. Tentukanlah nilai perbandingan untuk segitiga berikut
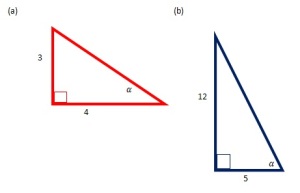
Jawab:
(a) Untuk sisi miringnya adalah
,
.
(b) Dengan langkah sebagaimana pada langkah (a), kita mendapatkan
,
.
2. Hitunglah nilai dari
.
Jawab:
.
.
.
.
.
3. Perhatikan ilustrasi berikut
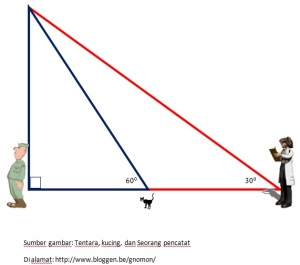
Jika Jarak antara kucing seorang pencatat dan kucing adalah 100 m, maka jarak Pencatat tersebut dengan seorang tentara sebagaimana gambar tersebut di atas adalah?
Jawab:
Perhatikan gambar di atas dengan diberikan tambahan keterangan sebagai berikut
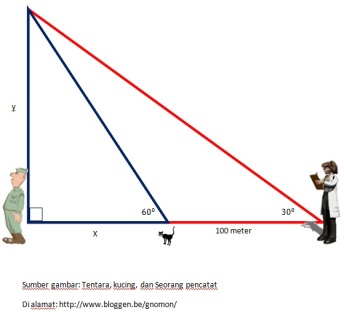
Ditanya berpakah panjang jarak ?
.
Jadi meter.
4. Tentukanlah perbandingan trigonometri jika
.
Jawab:
Perhatikan ilustrasi berikut
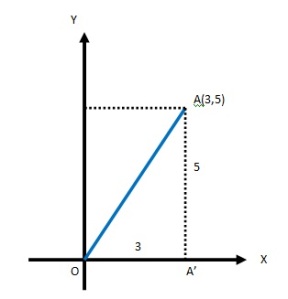
Dengan memandang ilustrasi gambar di atas kita mendapatkan , dengan menggunakan teorema pythagoras kita mendapatkan
.
.
C. Koordinat Kartesius dan Koordinat Kutub/Polar
Perhatikanlah ilustrasi berikut
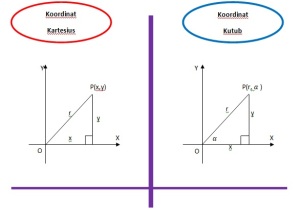
.
D. Perbandingan Trigonometri di Berbagai Kuadran
.
.
.
.
Perhatikan ilustrasi berikut
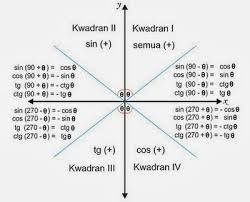
[Sumber]
Untuk sudut .
.
Perbandingan trigonometri untuk sudut negatif
.
.
1. Tanpa menggunakan tabel/kalkulator tentukanlah nilai jika diketahui
.
.
Jawab:
.
.
.
.
2. Tunjukkan bahwa
.
Jawab:
.
.
.
.
3. Diketahui koordinat kutub titik M adalah , maka koordinat kartesiusnya adalah….
Jawab:
.
E. Identitas Trigonometri
.
F. Fungsi Trigonometri
Perhatikanlah ilustrasi gambar berikut untuk grafik fungsi sinus dan cosinus
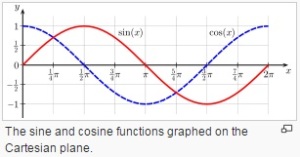
[Sumber]
Untuk fungsi tangen,
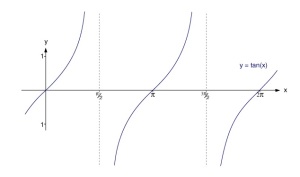
[sumber]
Fungsi Sinus , f(x)= sin x
.
Fungsi Cosinus , f(x)=cos x
.
Fungsi Tangen , f(x)=tan x
.
Untuk :
.
.
.
.
G. Persamaan Trigonometri Sederhana
.
.
1. Buktikan bahwa .
Bukti:
.
2. Tentukanlah himpunan penyelesaian dari persamaan .
Jawab:
.
Jadi Himpunan penyelesaiannya adalah = .
3. Lukislah grafik fungsi .
Jawab:
.
Untuk gambar silahkan pembaca melukiskannya sendiri sebagai latihan.
H. Aturan Sinus, Kosinus, dan Luas Segitiga
1. Aturan Sinus
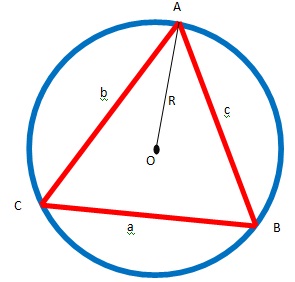
.
2. Aturan Kosinus
.
3. Luas Segitiga
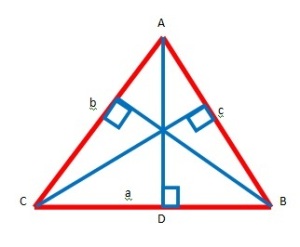
.
atau
.
atau
.
.
1. Diketahui dengan panjang sisi AC=10 cm dan BC=16 cm serta luas
, maka besar
jika sudutnya lancip adalah …
Jawab:
Diketahui , maka
.
2. Perhatikanlah gambar berikut
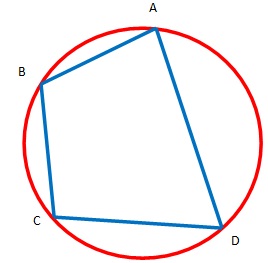
Jika , maka
adalah ….
Jawab:
Perhatikan kembali ilustrasi berikut
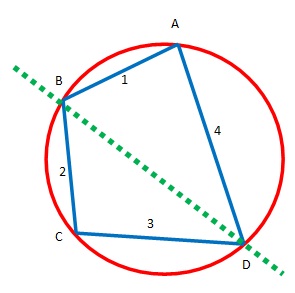
Langkah awal kita gunakan garis bantu BD untuk nantinya kita mendapatkan nilai cos dari sudut A, yaitu
.
Selanjutnya,
.
3. Carilah luas jika diketahui AB=10 cm, AC=14 cm dan BC=16 cm.
Jawab:
.
.
1. Perhatikanlah gambar berikut
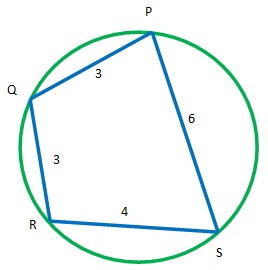
Tentukanlah nilai .
2. Perhatikanlah ilustrasi gambar berikut
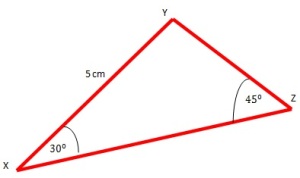
Carilah besar sudut dan panjang sisi yang belum diketahui dari segitiga di atas, kemudian cari pula luasnya?
3. (EBTANAS 2001) Diketahui luas segitiga ABC adalah . Jika panjang sisi
dan BC=7 cm, maka nilai
= ….
4. Diketahui seorang penerjun hendak mendarat secara vertikal sebagaimana ilustrasi berikut

Carilah harga x ?
5. Jika pada jajargenjang ABCD, dua diagonal panjangnya masing-masing 12 cm dan 16 cm dan sudut apitnya adalah , maka luas jajargenjang tersebut adalah ….
6. Diketahui , carilah
.
7. Buktikanlah bahwa
.
Tidak ada komentar:
Posting Komentar